6-9 二叉树的遍历 (25 分)
本题要求给定二叉树的4种遍历。
函数接口定义:
1
2
3
4
| void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
|
其中BinTree结构定义如下:
1
2
3
4
5
6
7
| typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
|
要求4个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
裁判测试程序样例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree CreatBinTree();
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
int main()
{
BinTree BT = CreatBinTree();
printf("Inorder:"); InorderTraversal(BT); printf("\n");
printf("Preorder:"); PreorderTraversal(BT); printf("\n");
printf("Postorder:"); PostorderTraversal(BT); printf("\n");
printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");
return 0;
}
|
输出样例(对于图中给出的树):
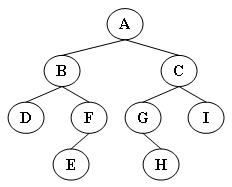
1
2
3
4
| Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
Levelorder: A B C D F G I E H
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree CreatBinTree();
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
BinTree CreatBinTree(){
BinTree BT = (BinTree)malloc(sizeof(struct TNode));
BT->Left=NULL;
BT->Right=NULL;
return BT;
}
int main()
{
BinTree BT = CreatBinTree();
printf("Inorder:"); InorderTraversal(BT); printf("\n");
printf("Preorder:"); PreorderTraversal(BT); printf("\n");
printf("Postorder:"); PostorderTraversal(BT); printf("\n");
printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");
return 0;
}
void InorderTraversal( BinTree BT ){
if(BT == NULL){
return;
}
InorderTraversal(BT->Left);
printf(" %c",BT->Data);
InorderTraversal(BT->Right);
}
void PreorderTraversal( BinTree BT ){
if(BT == NULL){
return;
}
printf(" %c",BT->Data);
PreorderTraversal(BT->Left);
PreorderTraversal(BT->Right);
}
void PostorderTraversal( BinTree BT ){
if(BT == NULL){
return;
}
PostorderTraversal(BT->Left);
PostorderTraversal(BT->Right);
printf(" %c",BT->Data);
}
void LevelorderTraversal( BinTree BT ){
BinTree Queue[1000];
int top = -1;
int tail = -1;
if(BT)Queue[++tail] = BT;
while(top<tail){
BinTree bt = Queue[++top];
printf(" %c",bt->Data);
if(bt->Left){
Queue[++tail] = bt->Left;
}
if(bt->Right){
Queue[++tail] = bt->Right;
}
}
}
|



